Pair approximation
In structured populations, finding analytical results is extremely difficult. Normally, models of evolutionary dynamics in lattices resort to Monte Carlo simulations. Pair approximation is one approach to try to replicate them, but via differential equations, without the need to run simulations (hauert2005).
We will focus on pairs of interacting players $p_{A,B}$, and all pairs connecting to A and B. The figure below shows an illustration of that, where x,y,z denotes the three connections of A and u,v,w the connections of B.
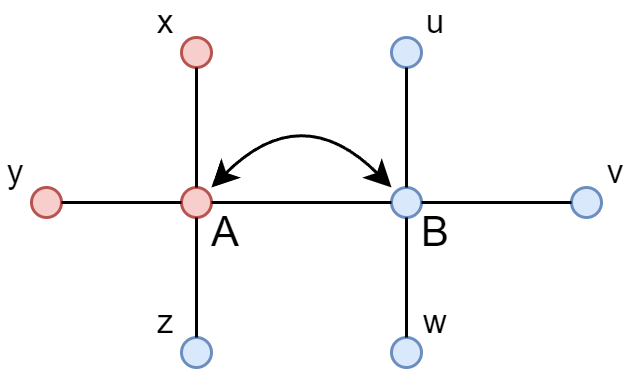
The transition probabilities are given by one strategy of a pair flipping $p_{A,B\rightarrow B,B}$, which is given by
\[\begin{align} p_{A,B\rightarrow B,B} = \sum_{x,y,z}\sum_{u,v,w} f(P_B - P_A) \times \frac{p_{x,A}\, p_{y,A}\,p_{z,A}\,p_{A,B}\,p_{u,B}\,p_{v,B}\,p_{w,B}}{p_A^3\,p_B^3} \end{align}\]where $f(P_B - P_A)$ is the probability of strategy adoption (normally the Fermi equation), and $p_{i,A}$ is the probability that the pair (i,A) have the strategy of A and the strategy of i given by the sum. With the sums, we consider all possible strategy pairs in all three directions of connections of each player interacting.
In the end, we need two differential equations, that are given by
\[\begin{align} \dot{p}_{c,c} = \sum_{x,y,z} \, [n_c(x,y,z)+1]\,p_{d,x}\,p_{d,y}\,p_{d,z} \sum_{u,v,w} p_{c,u}\,p_{c,v}\,p_{c,w}\,f(P_c(u,v,w)-P_d(x,y,z)) \\ - \sum_{x,y,z} \, n_c(x,y,z)\, p_{c,x}\,p_{c,y}\,p_{c,z}\sum_{u,v,w} p_{d,u}\,p_{d,v}\,p_{d,w}\, f(P_d(u,v,w)-P_c(x,y,z)) \end{align}\] \[\begin{align} \dot{p}_{c,d} = \sum_{x,y,z} \, [1 - n_c(x,y,z)]\,p_{d,x}\,p_{d,y}\,p_{d,z} \sum_{u,v,w} p_{c,u}\,p_{c,v}\,p_{c,w}\,f(P_c(u,v,w)-P_d(x,y,z)) \\ - \sum_{x,y,z} \, [2 - n_c(x,y,z)]\, p_{c,x}\,p_{c,y}\,p_{c,z} \sum_{u,v,w} p_{d,u}\,p_{d,v}\,p_{d,w}\, f(P_d(u,v,w)-P_c(x,y,z)) \end{align}\]The changes always come from a (d,c) interaction, since we are using imitation. In both equations, the first term is related to a defector changing to cooperation, and the second term a cooperator changing to defection.
Considering that the pair (A,B) changes from (d,c) to (c,c)
- we get $1+n_c$ new (c,c) and $1-n_c$ new (d,c) pairs
Considering that the pair (A,B) changes from (d,c) to (d,d)
- we lose $n_c$ pairs (c,c) and $2-n_c$ new (d,c) pairs
Code
1
2
3
4
5
6
7
8
9
# C. Hauert, S. György, Game theory and physics, Am. J. Phys. 73, 405 (2005)
# x u
# | |
# | |
# y ----- A ------ B ------ v
# | |
# | |
# z w
Parameters
1
2
3
4
5
6
7
8
9
10
11
12
13
using Plots, Printf,HomotopyContinuation, LinearAlgebra, DelimitedFiles, PlutoUI
begin
const K = 0.1
const k = 4
const R = 1.0
#const T = 1.1
const P = 0.0 #not used
const S = 0.0 #not used
# HomotopyContinuation
@var ρcc ρcd
end
Definitions
1
2
3
4
5
6
7
8
9
10
11
function W_fermi(ΔP, K)
return 1.0 / (1.0 + exp(-ΔP / K))
end
function payoff_C(nc, R, S)
return (nc+1)*R + (k - nc)*S
end
function payoff_D(nc, T, P)
return (nc+1)*T + (k - nc)*P
end
Master eq.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
function calculo_pho(ρ⃗, params)
T, R, P, S, K = params
eq_cc = 0.0
eq_cd = 0.0
# ρ₁₁ ρ₁₂ -> ρdd ρdc
# ρ₁₂ ρ₂₂ -> ρcd ρcc
p = [1.0-(ρ⃗[1]+2*ρ⃗[2]) ρ⃗[2];
ρ⃗[2] ρ⃗[1]]
for x in 0:1 # todas configuraçoes possiveis (D = 0 e C = 1)
for y in 0:1
for z in 0:1
for u in 0:1
for v in 0:1
for w in 0:1
nc_xyz = x + y + z
nc_uvw = u + v + w
Pc_xyz = payoff_C(nc_xyz, R, S)
Pc_uvw = payoff_C(nc_uvw, R, S)
Pd_xyz = payoff_D(nc_xyz, T, P)
Pd_uvw = payoff_D(nc_uvw, T, P)
Wcd = W_fermi(Pc_uvw - Pd_xyz, K)
Wdc = W_fermi(Pd_uvw - Pc_xyz, K)
A₁ = p[1,1+x]*p[1,1+y]*p[1,1+z]*p[2,1+u]*p[2,1+v]*p[2,1+w] #ρdi ρcj
A₂ = p[2,1+x]*p[2,1+y]*p[2,1+z]*p[1,1+u]*p[1,1+v]*p[1,1+w] #ρci ρdj
eq_cc += (nc_xyz+1)*A₁*Wcd - nc_xyz*A₂*Wdc
eq_cd += (1-nc_xyz)*A₁*Wcd - (2-nc_xyz)*A₂*Wdc
#@printf "%d %d %s\n" nc_xyz nc_uvw A₁
end
end
end
end
end
end
return eq_cc, eq_cd
end
Soluton
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
final_solutions = []
#T = 1.5
for T in 1.0:0.05:3.0
params = [T; R; P; S; K]
ρ⃗ = [ρcc; ρcd]
eq_cc, eq_cd = calculo_pho(ρ⃗, params)
# use HomotopyContinuation solve to solve polynomial system of equations
F = System([eq_cc,eq_cd])
result = solve(F; start_system = :polyhedral)
# filtering solutions
num_solutions = size(real_solutions(result))[1]
real_sol = real_solutions(result) # in function of ρcc
selected_solutions = Float64[] # in function of ρc now
# testar estabilidade com jacobiano simbólico
for i in 1:num_solutions
ρ₁₁, ρ₁₂ = real_sol[i] # ρcc, ρcd
ρc = ρ₁₁ + ρ₁₂ # ρcc + ρcd
ρd = 1.0 - ρc
#@printf "%f %f\n" ρc ρd
if ((0.0 ≤ ρ₁₁ ≤ 1.0) && (0.0 ≤ ρ₁₂ <= 1.0) && (ρc ≤ 1.0)
&& (0.0 ≤ ρd ≤ 1.0))
push!(selected_solutions, ρc)
re_eigs = real(eigvals(jacobian(F,[ρ₁₁,ρ₁₂])))
if re_eigs[1]<-1E-10 && re_eigs[2]<-1E-10
push!(final_solutions, (T, ρc))
end
@printf "---> %f %8.6f %8.6f %8.12e %8.12e\n" T ρc ρd re_eigs[1] re_eigs[2]
end
end
end